How do I deal with (diploma) Courses with several components?

Diploma Courses

This article explains how to deal with 14-19 Diploma or other courses with several components:

Options can:
-- handle courses that span across 2 or more Option Blocks, and
-- even if there are 2 or more TeachingGroups for each component of the course, it will ensure that the students are allocated consistently to the groups.

An advanced** example to illustrate:
A school has a 14-19 Diploma course which is to span across four of the five Option Blocks.
ie. a student will choose 5 subjects, of which 4 can be for the diploma.
A student must choose all of the diploma course components, or none.
 
      Step 1.
Suppose the 4 diploma parts are called Dip1, Dip2, Dip3, Dip4.
In this example we will complicate things by saying that there are two Teaching Groups for each of these, specified on the  Subjects Screen  like this: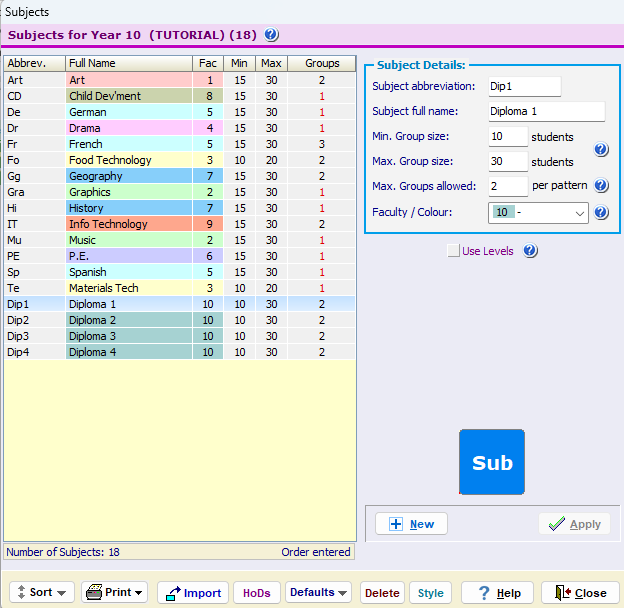So we will need to ensure (see below) that Options allocates the students consistently, so that each of the parallel groups remain separate and with the same membership for each of Dip1, Dip2, Dip3, Dip4.
(Note: if there is only one group for each 'subject' then everything is simpler!).

      Step 2.
If a student chooses Dip1, s/he must choose Dip2 and Dip3 and Dip4.
This can be ensured by using the Rules for Students' Choices Screen, by entering every possible pairing of the 4 groups, like this:      Step 3.
The Choices Screen will look like this: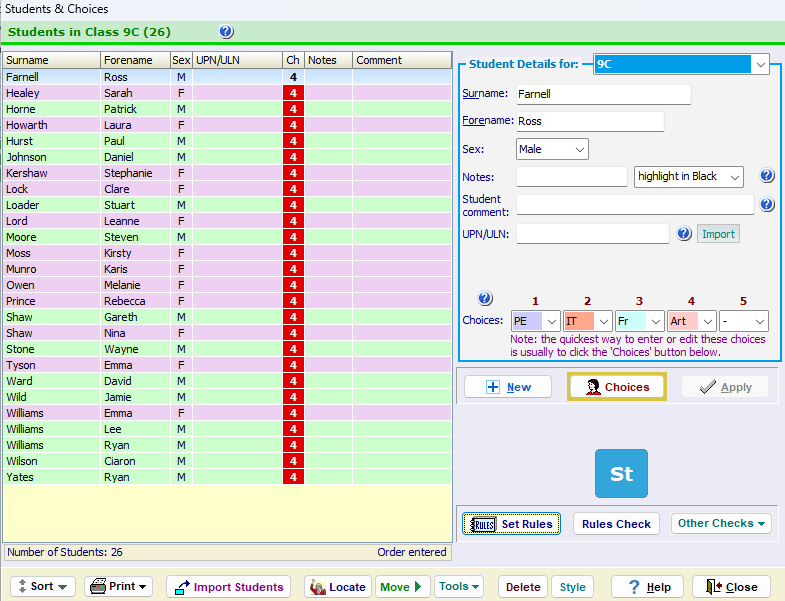      Step 4.
Before you can use the AutoCreate Screen to build up a Pattern, you need to tell Options that all of the students must be assigned to the groups consistently like this: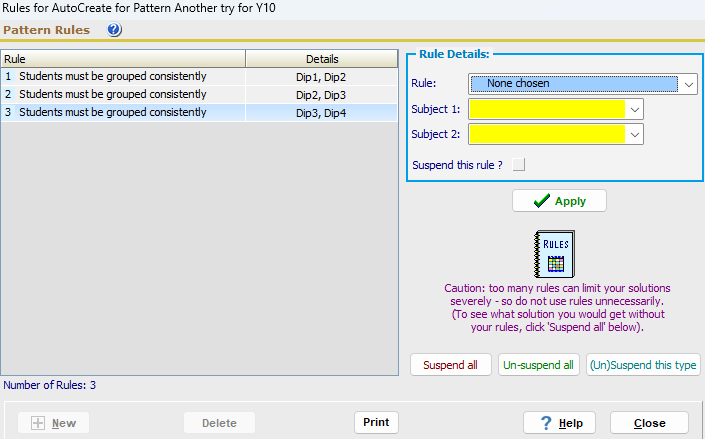Note: If there is only one group for each Subject (ie. each component of the course) then you do not need to use this rule.
Options will then look for solutions that obey these rules, when you click on Go:
**More general or simpler cases:
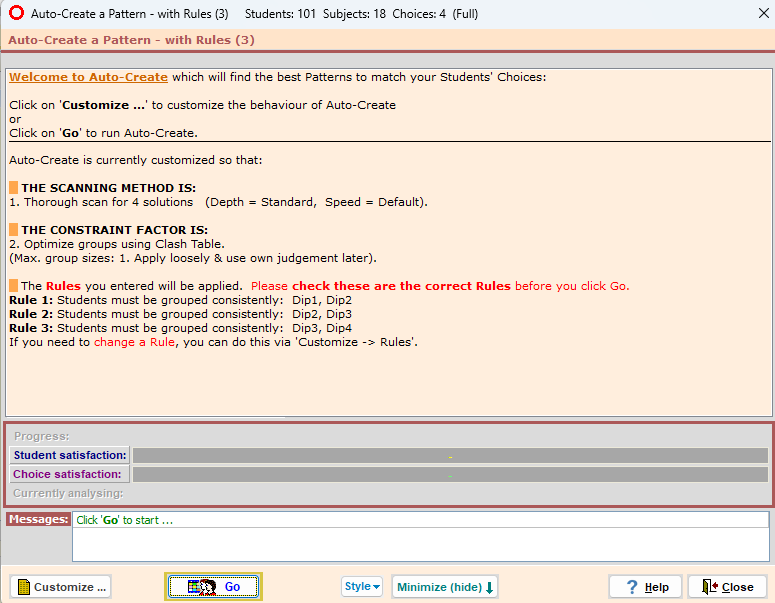
In this uncommon example we have used 4 diploma components, with 2 groups for each, and with the students to be assigned consistently.
In most cases the problem will not be this complicated.
The most usual case is 'double options' (eg. BTEC1 & BTEC2, or Double Maths at A-level).